데이터 분석을 위한 기본 수학(2)_ 문자식의 규칙,다항식 전개

📌 문자식의 규칙 (수학의 문자와 식 개념 정리)
문자식이란 수나 문자를 이용하여 어떤 규칙이나 관계를 나타낸 식입니다.
수학에서 패턴이나 규칙을 찾고 일반화할 때 문자식을 사용합니다.
1️⃣ 문자식의 기본 개념
📌 문자와 수의 조합
- 수(숫자)만 있는 식 → 3 + 5 , 2 × 4
- 문자가 포함된 식 → x + 3, 2a − 5 , 3m + 2n
📌 문자와 식의 역할
- 문자(변수): 변할 수 있는 값을 나타냄 → x,y,a,b
- 수(상수): 변하지 않는 값 → 3,5,−2,1.5
💡 예제
x+5
→ x 가 변하는 값이고, 5는 항상 같은 값!
2️⃣ 문자식의 규칙 정리
📌 (1) 덧셈과 뺄셈의 규칙
- 같은 문자는 계수(앞 숫자)끼리 계산 가능

- 다른 문자는 더하거나 뺄 수 없음

💡 예제

📌 (2) 곱셈과 나눗셈의 규칙
✔ 곱셈
- 문자끼리 곱하면 지수 형태로 표현

✔ 나눗셈
- 같은 문자는 지수를 빼서 표현

💡 예제

📌 (3) 분배법칙 (괄호 풀기)
- 곱셈이 괄호 안에 있을 때 분배해서 곱함

💡 예제
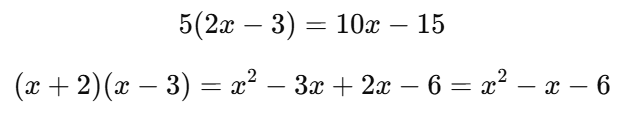
📌 (4) 문자의 대입 (규칙 찾기)
- 문자에 특정 값을 넣어 계산 가능
- 예를 들어 y = 2x + 3 x = 4를 대입

💡 예제

3️⃣ 문자식의 활용 예제
(1) 등차수열의 일반항
✔ 첫째항이 a, 공차가 d일 때, n번째 항은?

✅ 예제
✔ 1, 4, 7, 10, ...의 일반항 구하기

(2) 직사각형의 둘레와 넓이
✔ 가로가 , 세로가 일 때
- 둘레 :
- 넓이 : xy
✅ 예제
가로가 5a, 세로가 2b일 때
- 둘레: 2(5a + 2b) =10a + 4b
- 넓이: (5a) × (2b) = 10ab
(3) 삼각형의 넓이
✔ 밑변이 bb, 높이가 hh일 때
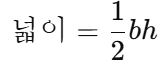
✅ 예제
밑변이 4x, 높이가 3y일 때
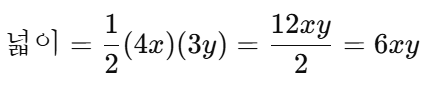
📌 분배법칙 (Distributive Law) 완벽 정리!
1️⃣ 분배법칙이란?
✔ 분배법칙이란?
하나의 값을 괄호 안에 있는 여러 항에 골고루 분배하여 곱하는 법칙이다.
a ( b + c ) = ab + ac
a ( b − c ) = ab − ac
즉, 괄호 바깥의 값(계수)을 괄호 안의 각 항에 곱해서 계산하면 됩니다!
2️⃣ 분배법칙의 기본 공식
📌 (1) 덧셈에 대한 분배법칙
a ( b + c ) = ab + ac
✅ 예제
3 ( 4 + 5 ) = 3 × 4 + 3 × 5 = 12 + 15 = 27
✅ 문자 포함 예제
x ( y + z ) = xy + xz
2a ( 3b + 4 ) = ( 2a × 3b ) + ( 2a × 4 ) = 6ab + 8a
📌 (2) 뺄셈에 대한 분배법칙
a ( b − c ) = ab − ac
✅ 예제
5 ( 7 − 2 ) = ( 5 × 7 ) − ( 5 × 2 ) = 35 − 10 = 25
✅ 문자 포함 예제
x ( y − z ) = xy − xz
4a ( 5b − 3c ) = ( 4a × 5b ) − ( 4a × 3c ) = 20ab − 12 ac
📌 (3) 다항식의 분배법칙 (곱셈 확장)
✔ 두 개의 다항식을 곱할 때도 분배법칙을 사용해요!

✅ 예제

✅ 또 다른 예제

📌 (4) 분배법칙을 이용한 식 정리
✔ 분배법칙을 활용하면 괄호를 없애고 식을 간단히 만들 수 있어요.
✅ 예제

✅ 또 다른 예제

3️⃣ 분배법칙 활용 문제
✅ 문제 1: 분배법칙을 이용해 전개하기

✔ 풀이

✅ 문제 2: 분배법칙을 이용해 식 정리하기

✔ 풀이

📌 다항식의 전개 (Polynomial Expansion)
1️⃣ 다항식 전개란?
✔ **다항식 전개(Polynomial Expansion)**란?
→ 괄호가 포함된 곱셈식을 분배법칙을 이용해 풀어서 전개하는 과정
💡 예제

➡ 분배법칙 적용:

2️⃣ 다항식 전개의 기본 규칙
📌 (1) 단항식과 다항식의 곱셈
✔ 단항식을 다항식에 곱할 때는 각 항에 분배법칙 적용
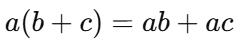
✅ 예제

📌 (2) 다항식과 다항식의 곱셈
✔ 두 개의 다항식을 곱할 때 각 항을 모두 곱해서 전개
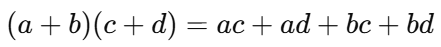
✅ 예제

➡ 각각 곱하기

✅ 또 다른 예제

📌 (3) 완전제곱식의 전개
✔ 같은 두 다항식의 곱셈 공식

✅ 예제

✅ 또 다른 예제

📌 (4) 합차 공식
✔ 두 개의 다항식이 서로 더하고 빼는 경우

✅ 예제

✅ 또 다른 예제

3️⃣ 다항식 전개 연습 문제
✅ 문제 1: 단항식과 다항식의 곱셈

✔ 풀이

✅ 문제 2: 다항식과 다항식의 곱셈

✔ 풀이

✅ 문제 3: 완전제곱식의 전개

✔ 풀이

✅ 문제 4: 합차 공식 활용

✔ 풀이

📌 더 복잡한 다항식의 전개 (고차 다항식 전개)
1️⃣ 복잡한 다항식 전개란?
✔ 단순한 다항식 곱셈을 넘어서, 세 개 이상의 괄호가 있는 경우 또는 차수가 높은 경우를 다루는 전개 방법.
✔ 기본적인 분배법칙과 공식(완전제곱식, 합차 공식 등)을 잘 활용하면 쉽게 풀 수 있다!
2️⃣ 복잡한 다항식 전개의 유형과 예제
📌 (1) 세 개 이상의 다항식 곱셈
✔ 두 개씩 먼저 전개한 후 마지막으로 남은 다항식을 곱한다.
✅ 예제 1

✔ 첫 번째로 두 개만 전개
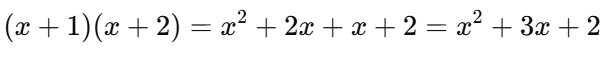
✔ 이제 나머지와 곱하기

각 항에 분배법칙 적용

✔ 결과:

✅ 예제 2

✔ 먼저 두 개 전개

✔ 이제 마지막과 곱하기

각 항에 분배법칙 적용

✔ 결과

📌 (2) 고차 다항식의 전개 (차수가 높은 다항식 곱셈)
✔ 차수가 높은 다항식도 차례대로 분배법칙을 적용해서 풀면 돼요!
✅ 예제 1

✔ 제곱 먼저 전개

✔ 이제 (x2 + 4x + 4) 에 (x + 2)를 곱하기

각 항에 분배법칙 적용

✔ 결과:

✅ 예제 2

✔ 제곱 먼저 전개
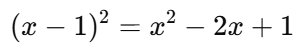
✔ 이제 (x2 - 2x + 1)에 (x - 1)를 곱하기

각 항에 분배법칙 적용

✔ 결과:

📌 (3) 네 개 이상의 다항식 곱셈
✔ 차례대로 두 개씩 곱하면서 풀면 됩니다!
✅ 예제

✔ 먼저 두 개 전개
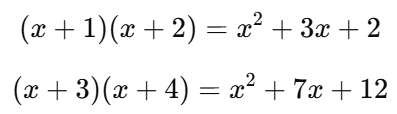
✔ 이제 두 결과를 다시 곱하기

각 항에 분배법칙 적용

✔ 결과:

🎯 결론: 다항식 전개 요약
✅ 단항식과 다항식의 곱셈 → 분배법칙 적용
✅ 다항식과 다항식의 곱셈 → 모든 항을 곱해서 정리
✅ 완전제곱식 공식 활용

✅ 합차 공식 활용

✅ 세 개 이상의 다항식 곱셈 → 두 개씩 먼저 전개
✅ 고차 다항식 전개 → 제곱부터 전개 후 분배법칙 적용
✅ 네 개 이상의 다항식 곱셈 → 두 개씩 차례대로 전개