데이터 분석을 위한 기본 수학(3)_분산,표준편차

📌 분산(Variance)
1️⃣ 분산의 정의
분산은 데이터가 평균으로부터 얼마나 퍼져 있는지를 나타내는 통계적 지표입니다.
이는 데이터의 변동성 또는 산포도를 측정하며, 값이 클수록 데이터가 평균에서 더 많이 흩어져 있음을 의미합니다.
✔ 분산(Variance, s)은 데이터가 평균을 중심으로 얼마나 퍼져 있는지를 나타내는 값입니다.
✔ 평균만으로는 데이터의 특징을 알기 어려우므로, 데이터의 흩어진 정도를 분석하는 것이 중요합니다.
2️⃣ 분산의 계산 방법
분산을 계산하는 단계는 다음과 같습니다:
- 평균 계산: 모든 데이터 값을 더한 후, 데이터의 개수로 나눕니다.
- 편차 계산: 각 데이터 값에서 평균을 뺀 값을 구합니다.
- 편차 제곱: 각 편차를 제곱하여 양수로 만듭니다.
- 제곱 편차의 평균 계산:
- 모집단 분산: 제곱된 편차의 합을 데이터 개수 n으로 나눕니다.
- 표본 분산: 제곱된 편차의 합을 n−1로 나눕니다. 이는 표본이 모집단을 대표하도록 보정하기 위함입니다.
수식으로 표현하면:
- 모집단 분산 :

- 표본 분산 s2:


3️⃣ 분산 구하는 방법
📌 분산 공식

- xi : 개별 데이터 값
- xˉ : 평균
- n : 데이터 개수
✅ 분산을 구하는 과정
- 데이터의 평균(Mean, xˉ)을 구한다.
- 각 데이터에서 평균을 뺀 값을 제곱한다.
- 제곱한 값들의 평균을 구한다.
4️⃣ 분산 예제
✅ 예제 1: 데이터가 2,4,6,8,10일 때 분산을 구해보자.
1단계: 평균 구하기

2단계: 각 데이터에서 평균을 빼고 제곱하기

3단계: 제곱한 값들의 평균 구하기

✔ 결과: 이 데이터의 분산은 8
5️⃣ 표준편차(Standard Deviation)
✔ 분산을 구하면 데이터의 퍼짐 정도를 알 수 있지만, 단위가 제곱 형태로 표현되므로 해석이 어려울 수 있습니다.
✔ 그래서 분산의 제곱근을 구한 값을 표준편차(Standard Deviation, )라고 합니다.
📌 표준편차 공식

✅ 위 예제에서 표준편차 구하기
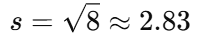
✔ 결과: 표준편차는 2.83
6️⃣ 분산과 표준편차의 의미
✔ 분산과 표준편차가 클수록 → 데이터가 평균에서 멀리 퍼져 있음
✔ 분산과 표준편차가 작을수록 → 데이터가 평균에 가까이 모여 있음
✅ 예제 비교
| 데이터 | 평균 | 분산 | 표준편차 |
| 2, 4, 6, 8, 10 | 6 | 8 | 2.83 |
| 5, 5, 6, 6, 6 | 5.6 | 0.24 | 0.49 |
💡 표준편차가 작은 데이터는 값들이 평균 근처에 많이 모여 있고, 큰 데이터는 다양하게 퍼져 있다는 의미입니다.
5️⃣ 분산의 의미와 활용
- 데이터의 변동성 측정: 분산은 데이터가 평균으로부터 얼마나 흩어져 있는지를 수치화하여, 데이터의 일관성 또는 변동성을 평가합니다.
- 품질 관리: 제조업 등에서는 제품의 품질 변동을 모니터링하고 관리하는 데 사용됩니다.
- 금융 분야: 투자 수익률의 변동성을 측정하여 리스크를 평가하는 데 활용됩니다.
📌 편차(偏差, Deviation)란?
1️⃣ 편차의 개념
✔ 편차(Deviation)란 개별 데이터 값이 평균(Mean)과 얼마나 차이가 나는지를 나타내는 값입니다.
✔ 즉, 각 데이터 값에서 평균을 뺀 값을 의미해요.
✅ 편차 공식
편차 = xi−xˉ
- xi : 개별 데이터 값
- xˉ : 평균
2️⃣ 편차 예제
✅ 예제 1: 데이터가 2,4,6,8,10일 때, 편차를 구해보자.
1단계: 평균 구하기

2단계: 각 데이터에서 평균을 빼기
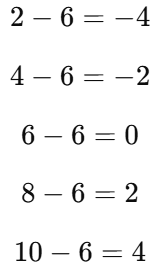
✔ 결과: 각 데이터의 편차 값은 -4, -2, 0, 2, 4
3️⃣ 편차의 특징
✔ 모든 편차 값을 더하면 항상 0이 된다.
( −4 ) + ( −2 ) + 0 + 2 + 4 = 0
✔ 편차 값이 클수록 평균에서 멀리 떨어져 있다.
✔ 편차의 제곱을 이용해 분산(Variance)을 구할 수 있다.
4️⃣ 편차와 관련된 개념
✅ 절대 편차(Absolute Deviation)
✔ 편차를 구할 때, 음수를 없애기 위해 절댓값을 취하는 방법

✅ 평균 절대 편차(Mean Absolute Deviation, MAD)
✔ 모든 절대 편차의 평균
