빅데이터 분석에 필요한 기본 수학(2)

📊 데이터 정리를 위한 기본 수학 개념

데이터를 효과적으로 정리하고 분석하려면 몇 가지 중요한 수학 개념을 이해하는 것이 필요합니다.

데이터 정리는 단순히 데이터를 정렬하는 것이 아니라, 데이터를 효율적으로 구조화하고, 패턴을 파악하고, 의미 있는 통계를 추출하는 과정입니다.

1️⃣ 기술 통계 (Descriptive Statistics)

데이터를 요약하고 정리하는 기법으로, 데이터를 한눈에 이해하는 데 도움을 준다.

🔹 대표값 (Measures of Central Tendency)

데이터의 중심이 어디에 있는지를 나타내는 값

• 평균(Mean): 데이터의 산술적 평균   ​
• 중앙값(Median): 데이터를 정렬했을 때 가운데 위치한 값
• 최빈값(Mode): 가장 자주 등장하는 값

평균

💡 예시: 평균 월급, 평균 키, 학생들의 시험 점수에서 가장 흔한 점수

🔹 산포도 (Measures of Dispersion)

데이터가 얼마나 흩어져 있는지를 나타냄

• 범위(Range): 최댓값 - 최솟값
• 분산(Variance, σ²): 데이터가 평균에서 얼마나 퍼져 있는지를 나타냄 
• 표준편차(Standard Deviation, σ²): 분산의 제곱근으로, 데이터의 변동성을 쉽게 해석할 수 있음 ​

분산

표준편차

💡 예시: 학생들의 시험 점수가 평균에서 얼마나 벗어나 있는지 측정

2️⃣ 데이터 정리와 변환 (Data Transformation & Preprocessing)

🔹 정규화 (Normalization)

데이터의 크기를 일정한 범위로 변환하여 분석을 쉽게 함

• 최소-최대 정규화 (Min-Max Scaling)

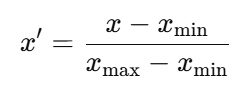
 → 0~1 범위로 데이터를 변환

• Z-점수 정규화 (Z-score Standardization)

• → 평균을 0, 표준편차를 1로 변환하여 비교 가능하도록 만듦

💡 예시: 머신러닝 모델에서 서로 다른 단위를 가진 데이터를 비교할 때 사용

🔹 이상치(Outlier) 탐지

이상치는 분석 결과에 큰 영향을 줄 수 있으므로 제거 또는 보정이 필요함

• 사분위수 범위(IQR, Interquartile Range) 활용

 

• • Q₁  (제1사분위수): 하위 25%
  • Q₃ (제3사분위수): 상위 75%
  • 이상치 기준: Q₁ - 1.5 × I QR   또는 Q₃ + 1.5 × I QR  바깥의 값

💡 예시: 급격하게 높은 매출 데이터, 비정상적으로 낮은 온도 측정값

3️⃣ 데이터 시각화를 위한 기본 개념

데이터를 정리한 후, 쉽게 이해할 수 있도록 시각화하는 것이 중요함.

• 히스토그램 (Histogram): 데이터의 분포를 시각화
• 상자 그림 (Box Plot): 이상치 탐지 및 데이터의 분포 비교
• 산점도 (Scatter Plot): 두 변수 간의 관계를 시각적으로 확인
• 파이 차트 (Pie Chart): 비율을 나타낼 때 유용

💡 예시: 웹사이트 방문자의 연령대 분포, 제품 판매량 비교

🔥 정리하면?

✅ 기술 통계를 활용해 데이터의 대표값과 변동성을 정리
✅ **데이터 변환(정규화, 표준화)**을 통해 데이터 분석이 용이하도록 변형
✅ 이상치 탐지를 통해 잘못된 데이터를 걸러냄
✅ 데이터 시각화를 통해 패턴과 인사이트를 쉽게 발견