빅데이터 분석에 필요한 기본 수학(3)_평균

📌 평균(Mean)

평균은 데이터의 중심값을 나타내는 대표적인 값이다.

데이터가 전체적으로 어디에 몰려 있는지를 이해하는 데 유용하며, 여러 가지 방법으로 계산할 수 있다.

1️⃣ 산술 평균 (Arithmetic Mean)

가장 기본적인 평균으로, 모든 데이터를 더한 후 개수로 나눈 값이다.

 

​

✅ 특징

✔ 데이터가 정규 분포(대칭적)일 때 대표값으로 적합
✔ 이상치(극단적인 값)의 영향을 크게 받음

💡 예제

시험 점수가 70, 80, 90, 100, 50인 경우

 

 

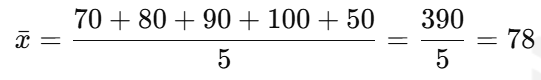
2️⃣ 가중 평균 (Weighted Mean)

각 값에 서로 다른 중요도를 부여할 때 사용하는 평균이다.

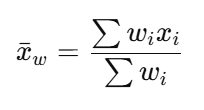
✅ 특징

✔ 각 데이터의 중요도를 다르게 반영할 수 있음
✔ 특정 항목이 더 중요한 경우 적용

💡 예제

시험에서 **중간고사(가중치 40%)**와 **기말고사(가중치 60%)**의 점수가 각각 80점, 90점이라면,

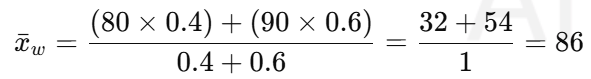
👉 단순 평균(85점)과 다른 결과가 나옴

3️⃣ 기하 평균 (Geometric Mean)

비율이나 성장률 데이터를 다룰 때 사용하는 평균이다.

​

✅ 특징

✔ 수익률, 성장률, 비율 데이터를 다룰 때 적합
✔ 극단적인 값(이상치)의 영향을 덜 받음

💡 예제

어떤 투자에서 10%, 20%, 30% 성장했다고 하면, 기하 평균은

👉 즉, 평균적으로 19.1%의 성장률을 가짐

 

4️⃣ 조화 평균 (Harmonic Mean)

속도나 비율을 다룰 때 유용한 평균이다.

​

✅ 특징

✔ 속도, 비율 데이터를 다룰 때 적절
✔ 작은 값이 강조됨 (큰 값보다 작은 값의 영향을 더 많이 받음)

💡 예제

한 사람이 50km/h로 1시간, 100km/h로 1시간 이동한 경우 평균 속도는?
산술 평균:

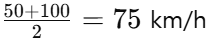
조화 평균:

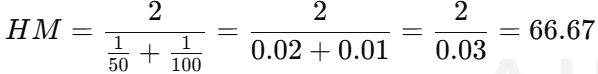
👉 실제 이동 거리와 시간을 고려하면 66.67km/h가 더 정확한 평균 속도

 

5️⃣ 절사 평균 (Trimmed Mean)

이상치(극단적인 값)의 영향을 줄이기 위해 일정 비율의 상위/하위 값을 제거한 후 계산하는 평균이다.

✅ 특징

✔ 극단적인 값의 영향을 줄임
✔ 스포츠 경기 점수(예: 피겨스케이팅)에서 자주 사용

💡 예제

점수: 20, 50, 80, 85, 90, 95, 100 (7개)

• 상위 10%, 하위 10% 제거 → 50, 80, 85, 90, 95 남음
• 평균: 

👉 극단적인 20점과 100점이 제외되면서 보다 신뢰할 수 있는 평균이 됨

 

🏁 정리: 언제 어떤 평균을 사용할까?

평균 종류 및 사용, 특징

산술 평균	일반적인 경우	이상치에 민감
가중 평균	데이터 중요도가 다를 때	중요도를 반영 가능
기하 평균	성장률, 수익률	이상치 영향이 적음
조화 평균	속도, 비율	작은 값의 영향을 더 많이 받음
절사 평균	이상치가 많을 때	극단값 제거 후 신뢰도 증가